Astro Meteorology is right !
Despite criticism that Thula Varsha or the North East Monsoon is far away, she is dot on time. It rained heavily in Trichur yesterday. It rained heavily in Madras the day before.
Tamil Nadu receives more rains than Kerala in this North East Monsoon phase. In Kerala rains are less this year, with the result we have unwanted power cuts.
We hope it pours heavily again. If not Kerala is in for more power cuts.
The N E Monsoon has a direct bearing on the economy, as Mr Monsoon is the Finance Minister of India !
NE Monsoon graces Kerala !
Despite criticism that Thula Varsha or the North East Monsoon is far away, she is dot on time. It rained heavily in Trichur yesterday. It rained heavily in Madras the day before.
Tamil Nadu receives more rains than Kerala in this North East Monsoon phase. In Kerala rains are less this year, with the result we have unwanted power cuts.
We hope it pours heavily again. If not Kerala is in for more power cuts.
The N E Monsoon has a direct bearing on the economy, as Mr Monsoon is the Finance Minister of India !
Kerala graced by N E Monsoon
Despite criticism that Thula Varsha or the North East Monsoon is far away, she is dot on time. It rained heavily in Trichur yesterday. It rained heavily in Madras the day before.
Tamil Nadu receives more rains than Kerala in this North East Monsoon phase. In Kerala rains are less this year, with the result we have unwanted power cuts.
We hope it pours heavily again. If not Kerala is in for more power cuts.
The N E Monsoon has a direct bearing on the economy, as Mr Monsoon is the Finance Minister of India !
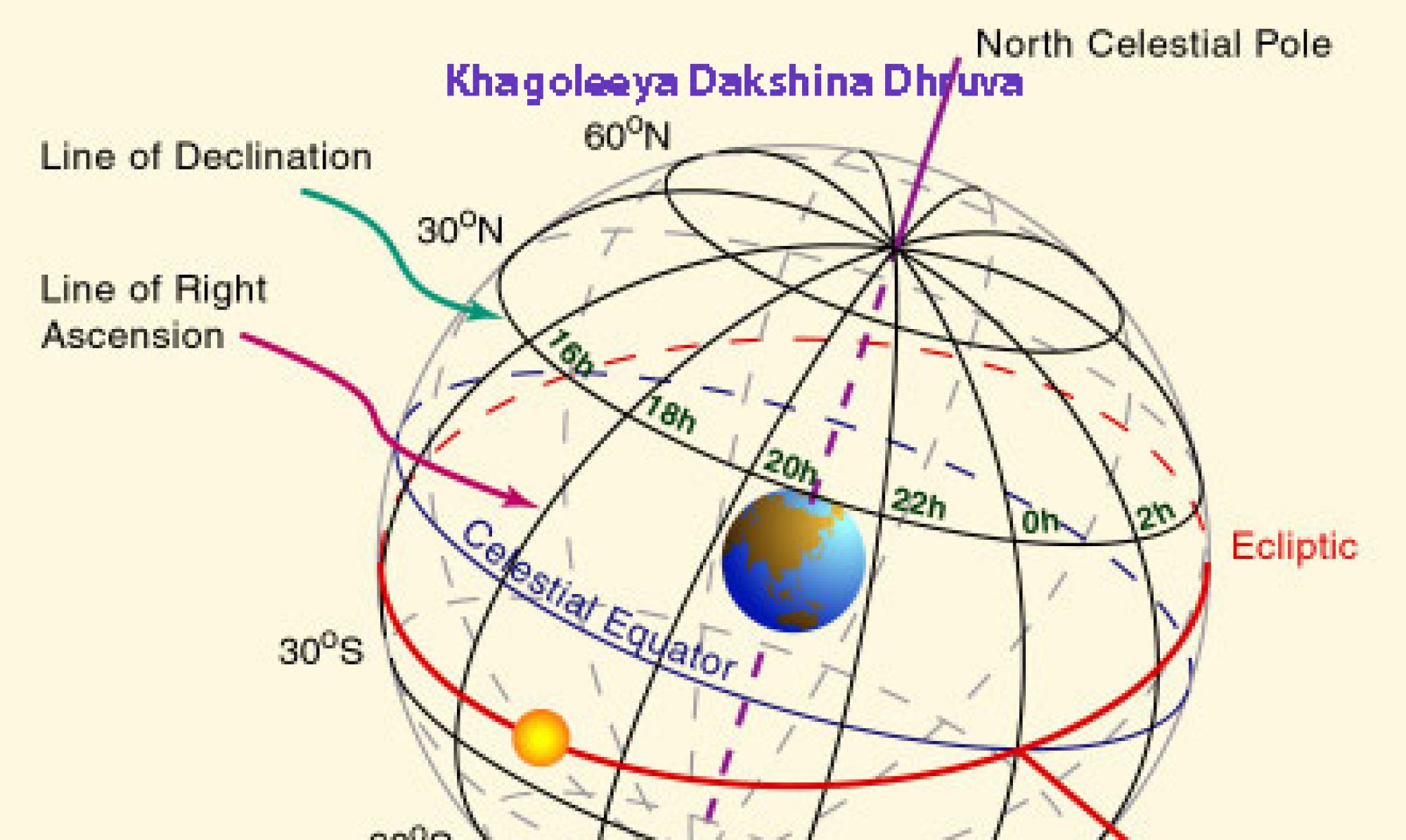
The Mathematical Ability of the Indians
I am convinced that everything has come down to us from the banks of the Ganges, – astronomy, astrology, metempsychosis,.. It is very important to note that some 2,500 years ago at the least Pythagoras went from Samos to the Ganges to learn geometry…But he would certainly not have undertaken such a strange journey had the reputation of the Brahmins’ science not been long established in Europe…
said Francois Marie Arouet Voltaire (French writer and philosopher)
Indians are a formidable software super power due to mathematical ability. Indians are the persons who saw beyond the Pythagorus Theorem
Perpendicular = Purusha
Base = Prakriti
Hypotenuse = Divine Man, Divya Purusha.
In Egyptian Symbolism,
Perpendicular = Orisis
Base = Isis
Hypotenuse = The Divine Child, Masonic Christ.
H^2 = a^2 + b^2
where H is the hypotenuse.
If 3 dimensional
h^2 = a^2 + b^2 + c^2
So the mathematical and philosophic ability of the Indians cannot be doubted, as they invented Zero.
The future is India’s !
Kerala lags behind !
Shaw’s definition of democracy ( Elected by Fools and ruled by rogues ) is true
of Kerla. Today is a total hartal day. Nobody is working. The Keralite gets one
more holiday in addtion to the 70 odd holidays he gets in one year. Kerala is
only 9th, with her GDP stagnating at around 58 billion.
Hartals have
become a common phenomenon. The Court banned Bandhs and so the politicians
replaced it by an other word, Hartal.
“It is a game of force and fraud
” said Veblen about democracy. It is a farce, as intuition and experience tell
us.
Now it is a open confrontation between two groups and God alone knows
what will happen.
When will India be liberated from this farce, which is goi in the name of democracy ?
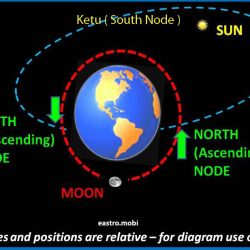
Time woke Thee up !
Poetic Imagery has it that the Lord was asleep in the Sleep of Superconscience ( Yoga Nidra ) when His own Temporal Power or the Power of Time awakened Him from His slumber !
Chathuryuganam cha sahasra mevam
Thvayi prasupthe punar advitheeye
Kalakhya shaktim pradama prasupta
Prabodhayatvam kila Visvanath !
Thy own Power Of Time, awakened Thee from Thy slumber !