Month: August 2011

Jyeshtadeva was a Kerala astronomer who helped in the calculation of longitudes, when there is latitudinal deflection. In his Yukti Bhasa, he calculates correctly the cos l, the cosine of latitude, which is important in the Reduction to the Ecliptic.

There is a separate section in the Yukti Bhasa, which deals with the effects of the inclination of a planet’s orbit on its latitude. He describes how to find the true longitude of a planet, Sheegra Sphutam, when there is latitudinal deflection.

“Now calculate the Vikshepa Koti, cos l, by subtracting the square of the Vikshepa from the square of the Manda Karna Vyasardha and calculating the root of the difference.”

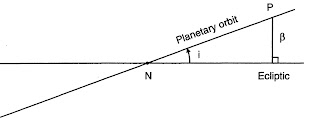
In the above diagram,

N is the Ascending Node

P is the planet on the Manda Karna Vritta, inclined to the Ecliptic

Vikshepa Koti = OM = SQRT( OP^2 – PM^2 )

Taking this Vikshepa Koti and assuming it to be the Manda Karna, sheegra sphuta, the true longitude, has to be calculated as before.

l, Vikshepa, is the Celestial Latitude, the latitude of the planet, the angular distance of the planet from the Ecliptic.

i is the inclination, inclinent of Orbit.

Sin l = Sin i Sin( Heliocentric Long – Long of Node ).

Celestial Latitude is calculated from this equation.

The longitude of the Ascending Node, pata, is minussed from the heliocentric longitude and this angle is called Vipata Kendra.

l, Vikshepa, is the Celestial Latitude, the latitude of the planet, the angular distance of the planet from the Ecliptic.

i is the inclination, inclinent of Orbit.

Sin l = Sin i Sin ( Heliocentric Long – Long of Node ).

Celestial Latitude is calculated from this equation.

The longitude of the Ascending Node, pata, is minussed from the heliocentric longitude and this angle is called Vipata Kendra.

l, Vikshepa, is the Celestial Latitude, the latitude of the planet, the angular distance of the planet from the Ecliptic.

i is the inclination, inclinent of Orbit.

Sin l = Sin i Sin( Heliocentric Long – Long of Node ).

Celestial Latitude is calculated from this equation.

The longitude of the Ascending Node, pata, is minussed from the heliocentric longitude and this angle is called Vipata Kendra.

In the last post we said that Angle AES is Sheegroccha, which is the longitude of the Sun. ( Sheegrocham Sarvesham Ravir Bhavathi ). The Angle AEK is the Heliocentric longitude of the planet.

Sidereal Periods of superior Planets in the Geocentric = Sidereal periods in the Heliocentric.

Sidereal Periods of Mercury and Venus = Mean Sun in the Geocentric

In the Planetary Model of Aryabhata, we find the equation

Heliocentric Longitude – Longitude of Sun = The Anomaly of Conjunction ( Sheegra Kendra ).

As Astronomy is Universal, we are indebted to these savants who made astro calculation possible. Even the word ” genius ” is an understatement of their brilliant IQ !

Development of the Planetary Models in Astronomy

Hipparchus 150 BCE

Claudious Ptolemy 150 ACE

Aryabhata 499 ACE

Varaha 550 ACE

Brahmagupta 628 ACE

Bhaskara I 630 ACE

Al Gorismi 850 ACE

Munjala 930 ACE

Bhaskara II 1150 ACE

Madhava 1380 ACE

Ibn al Shatir 1350 ACE

Paramesvara 1430 ACE

Nilakanta 1500 ACE

Copernicus 1543 ACE

Tycho Brahe 1587 ACE

Kepler 1609 ACE

Laplace 1700 ACE

Urbain Le Verrier 1850 ACE

Simon Newcomb 1900 ACE

E W Brown 1920 ACE

In the last post we said that Angle AES is Sheegroccha, which is the longitude of the Sun. ( Sheegrocham Sarvesham Ravir Bhavathi ). The Angle AEK is the Heliocentric longitude of the planet.

Sidereal Periods of superior Planets in the Geocentric = Sidereal periods in the Heliocentric.

Sidereal Periods of Mercury and Venus = Mean Sun in the Geocentric

In the Planetary Model of Aryabhata, we find the equation

Heliocentric Longitude – Longitude of Sun = The Anomaly of Conjunction ( Sheegra Kendra ).

As Astronomy is Universal, we are indebted to these savants who made astro calculation possible. Even the word ” genius ” is an understatement of their brilliant IQ !

Development of the Planetary Models in Astronomy

Hipparchus 150 BCE

Claudious Ptolemy 150 ACE

Aryabhata 499 ACE

Varaha 550 ACE

Brahmagupta 628 ACE

Bhaskara I 630 ACE

Al Gorismi 850 ACE

Munjala 930 ACE

Bhaskara II 1150 ACE

Madhava 1380 ACE

Ibn al Shatir 1350 ACE

Paramesvara 1430 ACE

Nilakanta 1500 ACE

Copernicus 1543 ACE

Tycho Brahe 1587 ACE

Kepler 1609 ACE

Laplace 1700 ACE

Urbain Le Verrier 1850 ACE

Simon Newcomb 1900 ACE

E W Brown 1920 ACE

In the last post we said that Angle AES is Sheegroccha, which is the longitude of the Sun. ( Sheegrocham Sarvesham Ravir Bhavathi ). The Angle AEK is the Heliocentric longitude of the planet.

Sidereal Periods of superior Planets in the Geocentric = Sidereal periods in the Heliocentric.

Sidereal Periods of Mercury and Venus = Mean Sun in the Geocentric

In the Planetary Model of Aryabhata, we find the equation

Heliocentric Longitude – Longitude of Sun = The Anomaly of Conjunction ( Sheegra Kendra ).

As Astronomy is Universal, we are indebted to these savants who made astro calculation possible. Even the word ” genius ” is an understatement of their brilliant IQ !

Development of the Planetary Models in Astronomy

Hipparchus 150 BCE

Claudious Ptolemy 150 ACE

Aryabhata 499 ACE

Varaha 550 ACE

Brahmagupta 628 ACE

Bhaskara I 630 ACE

Al Gorismi 850 ACE

Munjala 930 ACE

Bhaskara II 1150 ACE

Madhava 1380 ACE

Ibn al Shatir 1350 ACE

Paramesvara 1430 ACE

Nilakanta 1500 ACE

Copernicus 1543 ACE

Tycho Brahe 1587 ACE

Kepler 1609 ACE

Laplace 1700 ACE

Urbain Le Verrier 1850 ACE

Simon Newcomb 1900 ACE

E W Brown 1920 ACE

In the last post we said that Angle AES is Sheegroccha, which is the longitude of the Sun. ( Sheegrocham Sarvesham Ravir Bhavathi ). The Angle AEK is the Heliocentric longitude of the planet.

Sidereal Periods of superior Planets in the Geocentric = Sidereal periods in the Heliocentric.

Sidereal Periods of Mercury and Venus = Mean Sun in the Geocentric

In the Planetary Model of Aryabhata, we find the equation

Heliocentric Longitude – Longitude of Sun = The Anomaly of Conjunction ( Sheegra Kendra ).

As Astronomy is Universal, we are indebted to these savants who made astro calculation possible. Even the word ” genius ” is an understatement of their brilliant IQ !

Development of the Planetary Models in Astronomy

Hipparchus 150 BCE

Claudious Ptolemy 150 ACE

Aryabhata 499 ACE

Varaha 550 ACE

Brahmagupta 628 ACE

Bhaskara I 630 ACE

Al Gorismi 850 ACE

Munjala 930 ACE

Bhaskara II 1150 ACE

Madhava 1380 ACE

Ibn al Shatir 1350 ACE

Paramesvara 1430 ACE

Nilakanta 1500 ACE

Copernicus 1543 ACE

Tycho Brahe 1587 ACE

Kepler 1609 ACE

Laplace 1700 ACE

Urbain Le Verrier 1850 ACE

Simon Newcomb 1900 ACE

E W Brown 1920 ACE

In the above diagram,

A = Starting Point, 0 degree Aries
P = Planet
S = Sun
E = Earth

Angle AEK = Manda Sphuta, heliocentric longitude, after manda samskara
Angle AES = Sheegroccha, mean Sun, mean longitude of Sol
Angle AEP = True geocentric longitude of planet
Angle KEP = The Sheegra Correction or sheegra phalam

The Anomaly of Conjunction = Sheegra Kendra = Angle AES – Angle AEK

x = Angle AES – Angle AEK

Sin ( x ) =

r sin (x)
_______________________
¹^1/2

which is the Sheegra correction formula given by the Indian astronomers to calculate the geocentric position of the planet.

1. R + r cos x)^2 + rsin x^2 [↩]

In the above diagram,

A = Starting Point, 0 degree Aries
P = Planet
S = Sun
E = Earth

Angle AEK = Manda Sphuta, heliocentric longitude, after manda samskara
Angle AES = Sheegroccha, mean Sun, mean longitude of Sol
Angle AEP = True geocentric longitude of planet
Angle KEP = The Sheegra Correction or sheegra phalam

The Anomaly of Conjunction = Sheegra Kendra = Angle AES – Angle AEK

x = Angle AES – Angle AEK

Sin ( x ) =

r sin (x)
_______________________
¹^1/2

which is the Sheegra correction formula given by the Indian astronomers to calculate the geocentric position of the planet.

1. R + r cos x)^2 + rsin x^2 [↩]