Vedic Astronomy & Trignometry
In the Great Circle of Light which is 360 degrees, ( the Bha Chakra, the Kala Chakra, the Zodiac ), the first 90 degrees are Oja Pada ( Odd Tri Signs ) and the next 90 degrees are Yugma Pada ( Even Tri Signs ).
There are two major Indian Planetary Models - the Eccentric Model and the Epicycle Model. In the Eccentric Model, the Mean Circle is called Manda Pratimandala, that is the circle traversed by the mean angular motion of the planet. In the Epicycle Model, the Planet is on the epicycle, known as Manda Paridhi.
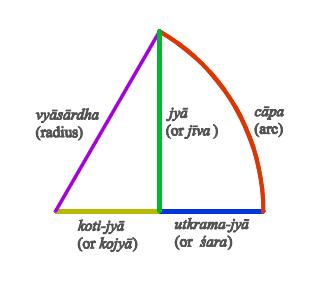
The Equation of Bhuja
|
|
The degrees traversed by a planet is called Bhuja and the degrees yet to be traversed by a planet is called Koti in an Odd Sign. In an Even Sign, the degrees traversed by the planet is called Koti and the degrees yet to be traversed by a planet is called Bhuja. In other words, the degrees traversed by a planet is the same in the first 0 - 90 degrees and in the second Pada, it is 180 - degrees traversed. In the 180-270 degrees arc, it is distance traversed - 180 degrees and in the 270-360 degrees arc, it is 360 - distance traversed. This is known in Vedic Astronomy as the equation of Bhuja or Sine. Bhujajya is radius multiplied by modern Sine.
( Oja Yatra Bhujaira Kotirapara Meshadi Jookadhi Kau )
Brahmagupta, in his mathematical treatise, the Brahmasphuta Siddhanta used the word Jya which means 5 degrees of a 360 degree circle which is the Zodiac, which is the Ecliptic. Suppose a planet has traversed 42 degrees in the first Oja Pada ( From Aries to Gemini end ).The Bhuja is 42 degrees and the Bhujajya is the 9th Jya or the 9*5 th degree. Bhujajya by Trijya is Opposite Side by Hypotenuse or the modern Sine.
|
|
Jya Ganitha means Trignometry. The equation for Koti is different. It is Kotijya by Trijya or Adjacent Side by Hypotenuse ( the modern Cos ). As per Indian Learning it was Aryabhata, one of the greatest mathematicians ever, who first computed the celestial longitudes of planets ( Aryabhato Graha Ganitham ).
The calculations given for the perturbations of Moon, Jupiter and Saturn are as follows. First find out the Bhuja of the planet, the degrees traversed. Find out its Bhujajya or Sin ( Bhuja ). Multiply it by the value given ( which is in seconds) and add it to the mean longitude of the planet.
Meshadi , Thuladi, Karkyadi & Makaradi ( The First Points of Aries, Cancer, Libra & Capricorn )
From Aries to Libra is the Northern Celestial Hemisphere ( NCH ) and from Libra to Aries is the Southern Celestial Hemisphere ( SCH ). If the planet's Kendra is in NCH, the values are to be subtracted and if in the SCH, it is to be added. ( Meshadi Rinam, Thuladi Dhanam )
Karkyadi is the First Point of Cancer and the beginning of Dakshinayana, the Southern course of the Sun, his declination South. Makaradi is the First Point of Capricorn and the beginning of Uttarayana, the Northern course of the Sun , his declination North. At Meshadi, the Sun's declination is 0 degrees and Right Ascension is 0 degrees. At Karkyadi, the Sun's declination is +23 degrees 27 minutes and Right Ascension is 90 degrees. At Thuladi, the Sun's declination is 0 degrees and Right Ascension is 180 degrees. At Makaradi, the Sun's declination is -23 degrees 27 minutes and Right Ascension is 270 degrees.
The Perturbations of Jupiter
The equations given for Jupiter's perturbations are as follows: Five major perturbations are included along with a major perturbation which is given below. ( The great Jupiter - Saturn perturbation ).
Kendra means an angle in Sanskrit . Manda Kendra means Mean Anomaly, the angle between position and aphelion and Sheeghra Kendra is the angle between position and the Earth Sun Vector. All Kendras are zero at perihelion. Perihelion is taken as 0 degrees and Aphelion is 180 degrees.
The Great Jupiter Saturn
Perturbation. ( Amplitude .332 degrees, Duration, Period = 918 years
)
The English Era + 3102 gives the Kali Era, the Era of the Hindu Calender. Add 3102 to the Year of Birth to get the Kali Year of Birth. From that value 4660 is deducted and the value is divided by 918. This gives the Beeja Kendra. Find out the Sin ( Bhuja ) of that, multiply it with 1187 seconds and add it to Jupiter's longitude if the Kendra is in NCH and subtract it if it is in SCH.
The differential equation for that is
If Kali Year of birth is xyear
m = 1187 secs*( Sin ( xyear - 4660) * 360/918)
If m is in SCH, M = M - m
If m is in NCH, M = M +m , where M is the Mean Longitude of Jupiter
There are other minor perturbations which can be ignored.
( Lj = Mean Longitude of Jupiter; Ls - Mean Longitude of Saturn. These longitudes are Tropical or Sayana. ).
| First Kendra | (Sin ( Lj - Ls ) - 1. 15)* 81 |
| Second Kendra | Sin (( Lj - 2 Ls) - 13.08 )* 132 |
| Third Kendra | Sin ( 2 Lj - 2 Ls - 0.58 )* 200 |
| Fourth Kendra | Sin ( 2 Lj - 3 Ls - 61.57 )* 83 |
| Fifth Kendra | Sin ( 3 Lj - 5 Ls - 56.38 )* 162 |
The first value is to be added if the Kendra is Thuladi ( after the First Point of Libra ) and deducted if it is Meshadi ( after the First Point of Aries ). 2,3,4 & 5 are to be added if it is Meshadi and subtracted if Thuladi
The Perturbations of Saturn
The Great Jupiter Saturn Perturbation. ( Amplitude 2783 sec, Duration, Period = 918 years )
The English Era + 3102 gives the Kali Era, the Era of the Vedic Calender. Add 3102 to the Year of Birth to get the Kali Year of Birth. From that value 4660 is deducted and the value is divided by 918. This gives the Beeja Kendra. Find out the Sin ( Bhuja ) of that, multiply it with 2783 seconds and add it to Saturn's longitude if the Kendra is in NCH and subtract it if it is in SCH.
The differential equation for that is
If Kali Year of birth is xyear
m = 2783 secs*( Sin ( xyear -4660) * 360/918)
If m is in SCH, M = M - m
If m is in NCH, M = M +m , where M is the Mean Longitude of Saturn
| First Kendra | Sin ( Lj - 2 Ls ) -14.66 )*418 |
| Second Kendra | Sin ( 2 Lj - 4 Ls + 56.90 )* 667 |
| Third Kendra | Sin ( 3Ls - Lj + 77.38 )* 48 |
These values are to be added if the Kendra is Thuladi ( after the First Point of Libra ) and deducted if it is Meshadi ( after the First Point of Aries ). In Sanskrit it is called Meshadi Rinam & Thuladi Dhanam. Meshadi is the beginning of the Northern Celestial Hemisphere and Thuladi the begining of the Southern Celestial Hemisphere.
There are other minor perturbations which may affect only the Vikala ( second ) of the planet's longitude and hence can be ignored.
|
|
The Perturbations of the Moon
(Ms - Mean Anomaly of the Sun; Mm - Mean Anomaly of the Moon; Ls - Mean Longitude of the Sun; Lm - Mean Longitude of the Moon; D = Lm - Ls ( Thidhi); Nm - Node of the Moon. These values are Sidereal or Nirayana )
14 Kendras are to be made and 14 trignometric corrections are to be given, according to astronomical savants. These 14 reductions are mandatory and only after these reductions can we get the true longitude of the Moon.
| First Kendra | Sin ( Ms + 180 ) * 658 |
| Second Kendra | Sin ( Lm - Ls ) * 121 |
| Third Kendra | Sin ( 2*D - Mm ) * 4467 |
| Fourth Kendra | Sin ( 2*D + 6 Signs ) * 2145 |
| Fifth Kendra | Sin (( 2*D - Mm -Ms ) + 180)* 198 |
| Sixth Kendra | Sin ( 2*D - Ms ) * 155 |
| Seventh Kendra | Sin ( Mm- Ms + 180 ) *112 |
| Eighth Kendra | Sin ( 2( Lm - Nm- Mm +180))* 85 |
| Ninth Kendra | Sin ( 2*Ls - Nm ) * 81 |
| Tenth Kendra | Sin ( Mm - Ms )* 73 |
| Eleventh Kendra | Sin ( 2*D + Mm ) * 60 |
| Twelfth Kendra | Sin ( 2*Mm - 2 D + 180 ) * 42 |
| Thirteenth Kendra | Sin ( 4*D - Mm ) * 35 |
| Fourteenth Kendra | Sin ( 4*D - 2*Mm +180)* 30 |
These trignometric corrections should be added to Moon's Mean Longitude if the Kendra is in the Southern Celestial Hemisphere and deducted if the Kendra is in the Northern Celestial Hemisphere and then we get the Samskrutha Chandra Madhyamam or the Cultured Mean Longitude of the Moon. Manda Kriya ( Reduction to True Anomaly ) must be done. Then Parinathi Kriya ( Reduction to Ecliptic ) should be done and what we get then is the longitude of the Moon along the Ecliptic !
Viskshepa Vrittopa Gatho
Vipatha
Thasmannayel Jyam Parinathyabhikhyam
Yugmaupada Swarnam Idam Vidheyam
Syath Kranti Vritteeya Ihaisha Chandra !
After the Reductions Fourteen, Sin M to be added or minussed
To the Cultured Longitude Mean; The Node to be deducted &
Reduced to the Earth's Path ( Ecliptic ); thus shall we get resultant
Value,
Luna's true Sidereal Longitude !
References
|
|
The 18 Siddhantas, named after 18 Seers
Surya Siddhanta
Pitamaha Siddhanta
Vyasa Siddhanta
Vasishta Siddhanta
Atri Siddanta
Parasara Siddhanta
Kashyapa Siddhanta
Narada Siddhanta
Garga Siddhanta
Marichi Siddhanta
Manu Siddhanta
Angira Siddhanta
Lomasa Siddhanta
Paulasa Siddhanta
Yavana Siddhanta
Chyavana Siddhanta
Bhrigu Siddhanta
Brahma Siddhanta
And Others
Maha Bhaskareeya by Bhaskara I
Arya Siddhanta by Aryabhata I
Maha Siddhanta by Aryabhata II
Siddhanta Siromani by Bhaskara II
Aryabhateeya by Aryabhata
Aryabhateeya Bhasya by Neelakanta Somayaji
Sphuta Nirnaya by Achyuta Pisharodi
Siddhanta Darpana by Neelakanta
Ganitha Adhyaya by Bhaskara
Ganith Nirnaya by Puliyoor
Brahma Sphuta Siddhanta by Brahmagupta
Siddhanta Shekhara by Sripathi
Siddhanta Tatva Viveka by Kamaleswara
Siddhanta Darpana by Neelakanta
Siddanta Deepika by Parameswara
Tantrasangraha by Neelakanta
Venvaroha by Madhava
Yukthi Bhasha by Jyeshta Deva
Laghu Manasa by Munjala
Badha Deepika by Parameswara