| Sun | 11 | 28 | 33 | 50 | 44 |
| Moon | 0 | 29 | 40 | 21 | 1 |
| Moon's Apogee | 3 | 12 | 39 | 15 | 19 |
| North Node | 8 | 10 | 38 | 45 | 40 |
| Mars | 4 | 13 | 45 | 4 | 40 |
| Mercury | 5 | 11 | 38 | 31 | 41 |
| Jupiter | 6 | 13 | 47 | 42 | 7 |
| Venus | 8 | 19 | 49 | 11 | 32 |
| Saturn | 7 | 25 | 20 | 11 | 55 |
| M =
Mean Anomaly of the planet;
A = Aphelion of the Planet ;
L = Mean Longitude of the Planet; e = orbital
eccentricity; mjv = orbital eccentricity in seconds; Sheegra Kendra
= The Anomaly of Conjunction;
Sheegroccha = Perihelion; Mandoccha = Aphelion; Sheeghra Phala
= The Angle between the Planet, the Sun and Earth; Oja = Odd; Yugma = Even; Manda Kendra =
The angle between position and Aphelion; Sheeghra Kendra Ardha = A/2, half of Sheegra Kendra;
Kranti Vritta = Ecliptic; Vikshepa Vritta = Heliocentric Circle;
Kshithija = Celestial Horizon; Bha Chakra = Zodiac; Vishuvat Vritta =
Celestial Equator; Khagoleeya Dhruva Rekha = Celestial Meridien;
Vishu Vat Bhoga = Right Ascension( R A ); Meshadi = The First
Point of Aries; Thuladi = The First Point of Libra; Karkyadi = The First
Point of Cancer; Makaradi = The First Point of Capricorn; Theta = True
Longitude of the planet; v = True Anomaly; Manda Karna = Radius Vector,
heliocentric distance; Sheeghra Karna = geocentric vector, distance of the
planet from the earth; Ravi Manda Karna = Sun's distance; Nathamsa =
Altitude of the Planet; Digamsa = Azimuth. Bhaga, Kala, Vikala =
Deg, Mins, Secs; Madhyama Manda Karna = Average Vector; Patha = Node;
Thidhi - D or Day or Lunar Day, the first Lunar Day being the Moon within
12 degrees of the Sun; Vara - Day of the Week; Bhujajya = R Sin; Kotijya =
R Cos; Sparsajya = Tan; Sparsachapa= Atan; Bhujachapa = Asin; Kotichapa =
Acos; Pranakalanthara= Difference between Tropical Longitudes and R A;
Kala Hora = Planetary Hours; Hora = Hour; Chara Jya = Sin C; Manda Jya =
Sin M; Parinathi Jya = Sin h; Guru Sani Karsha - Perturbations of
Jupiter and Saturn; Chandra Karsha - Perturbations of the Moon;
Chathurdasa Jya Samskaras - 14 trignometric corrections to the Moon;
Vikshepa - Celestial Latitude; Kranti - Declination; Dhruva = R A ; Sphuta
= Celestial Longitude; Indra - Uranus; Varuna = Neptune; Rudra = Pluto;
Kala = Phobos; Mrityu = Deimos; Gulika = Titan; Yamakandaka = Ganymede;
Vipatendu = Mean Longitude of the Moon - Node of the Moon ; Manda Karna -
heliocentric distance; Sheegra Karna - geocentric distance of the
planet, Parama Vikshepa/ Sara - the angular distance of the orbital plane from
the Ecliptic Parama Manda Karna - Maximum Vector, Laghu Manda Karna
- Minimum Vector ; Vipata Kendra - the angle between Position and the
Node; Sheegra Kendra - the angle between Position of the planet and the
Earth Sun Vector.
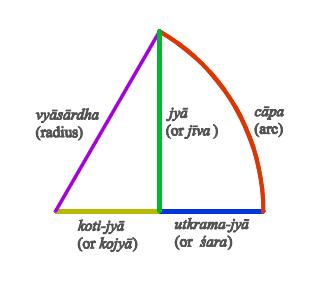
Sara - Reverse Sine, 1-cos x, Chapa - Arcsine. The Arcsine resembles a Bow,Chapa and Versine, Arrow, Sara, according to the Indian mathematicians ! The Three Methods of Vedic Astronomy & Mathematics
1) Zodiacal Longitudes - The First Method is to compute the longitudes of the planets along the Ecliptic ( Kranti Vritta ). Western astronomers have accepted 0 degree Aries as the First Point of the Tropical Zodiac and Vedic astronomers have accepted 0 degree Beta Arietis ( Aswini ) as the First Point of the Sidereal Zodiac. Extending 9 degrees to either side of the Ecliptic is the Great Circle of Light, the Zodiac.
2) Celestial Equatorial Longitudes - The Second Method is to compute the longitudes along the Celestial Equator ( Vishuvat Vritta ). The Starting Point is 0 degree Aries. The longitudes thus obtained is called the Right Ascension ( R A ) of Planets.
3)Celestial Horizontal Longitudes - The Third Method is to compute longitudes along the Celestial Horizon. The Eastern Celestial Horizon, the intersecting point between the Ecliptic and the Celestial Horizon, is called the Ascendant ( Udaya Lagna ). 180 degrees opposite to that point is called the Western Celestial Horizon ( Astha Lagna ). The highest point on the Celestial Horizon is called the Zenith ( Madhya Lagna or MC ) and the lowest point, the Nadir ( Patala Lagna or IC ). The Original Point of the Celestial Horizon is the Northern Point on the Celestial Horizon.
The Vedic Method is Longitude corrected thrice, through 3 major trignometric corrections called Manda Kriya ( Reduction to True Anomaly ) Parinathi Kriya ( Reduction to Ecliptic ) & Sheeghra Kriya ( Reduction to Geocentric Coordinates ).
Reduction to the Heliocentric Coordinate System
I . Reduction to True Anomaly ( Manda Kriya ) After finding the Mean Longitude of the Planet, the Mean Anomaly of the Planet is calculated as per the formula Mean Anomaly = Mean Longitude - Aphelion ( M = L - A ). The Manda Jya Vikalakal ( mjv , eccentricity in seconds ) is computed as per the formula mjv = R (2 e - 1/4 e^3 + 5/95 e^5 ) Sin A + R (5/4 e^2 - 11/24 e^2 + 17/192 e^2 ) Sin 2 A + R ( 13/12 e^3 - 43/64 e^5 ) Sin 3 A + R ( 103/ 96 e^4 - 451 / 480 e ^5 ) Sin 4 A + R ( 1097/960 e ^5 ) Sin 5 A + R (1223/960 e ^ 6 ) Sin 6 A A = Mean Anomaly of the Planet + 6 Signs or M + 180. R is 206265 seconds This value MJV is deducted or added to M, the Mean Anomaly of the Planet to get the True Anomaly of the planet, v v = M + or - mjv If the Mean Anomaly ( Manda Kendra ) is greater than 6 Signs, it is added and if it is less than 6 Signs ( 180 degrees ), it is subtracted. The Radius Vector ( Manda Karna ) is computed using the formula Manda Karna = a ( 1+ 1/2 e^2 ) - e ( 1- 3/8 e^2) Cos A - 1/2 e^2 ( 1- 2/3 e^2 ) Cos 2 A - 3/8 e^3 Cos 3 A - 1/3 e^4 Cos 4 A ) where a is the semi major axis ( Madhyama Manda Karna ) of the planet. Semi Major Axis is the average distance of the planet expressed in AU. The Sun's a is 1 AU or 149 million kilometres from the earth. It is to be noted that at 90 degrees the Manda Karna of the planet equals Semi Major Axis because Cos 90 = 0.
Reduction to the Ecliptic Coordinate System
II. Reduction to the Ecliptic ( Parinathi Kriya )
The Ascending Node of the planet is deducted to get the Y, the planet minus the Node. Y = True Anomaly of the Planet - Node of the planet
First the latitude of the planet is computed as per the formula Sin l = Sin L Sin Y where l is the latitude of the planet, Y is the Longitude of the planet after deducting the Node and L is the maximum latitude of the planet The mean longitude of the planet after Manda Kriya is reduced to the Ecliptic Coordinate System . The formula used is Sin h = ( 1-Cos L Sin Y Cos Y /cos l ) where the l is the latitude of the planet, Y is the Longitude of the planet after deducting the Node and L is the maximum latitude of the planet and h is the Parinathi Phalam, the factor which is to be added or subtracted to the True Anomaly. ( This is also the formula used for computing the Sun's Pranakalanthara which is the difference between Tropical longitudes and Right Ascension ). i or Inclination or inclinent of Orbit, is known as Parama Vikshepa, the angular distance of the orbital plane from our plane of reference, the Ecliptic. This is also known as Sara. For Mercury, it is 7 degrees and for Jove it is 1.31 degrees. The first 3 Signs are Odd ( Oja ), the next 3 Signs are Even ( Yugma ), the next 3 Signs are Odd ( Oja ) and the next 3 signs are Even ( Yugma ). The Parinathi Phalam is added if the Signs are Yugma and subtracted if it is Oja to True Anomaly to get the Ecliptic degree. Ecliptic Degree = True Anomaly + or - Parinathi Phalam The Heliocentric distance or Manda Karna ( Kranthi Vritheeya Manda Karna ) is computed as per the formula
Kranthi Vritheeya Manda Karna = Vikshepa Vritheeya Manda Karna * cos l
Reduction to the Geocentric Coordinate System
III Sheeghra Kriya - Reduction to Geocentric Coordinates
The Sheeghra Anomaly When the longitude of the Sun is deducted from the Ecliptic Degree thus obtained, we get the Sheeghra Anomaly, the angle between the Sun and the planet Sheeghra Anomaly = Heliocentric longitude of planet - Longitude of the Mean Sun. x, Sheeghra Phalam is the angle formed between the Sun, the planet and the Earth. It is computed as per the formula Tan A/2 - x = ( b - a) /( b + a) Tan A/2 where A is the Sheeghra Kendra, a is the Ravi Manda Karna ( Sun's distance ), b the Graha Manda Karna ( distance of the planet from the Sun ) and x the Sheeghra Phalam
Arka Sphutoniham Kheda Mandasphuta mihoditham
The Sheeghra Phalam is added if the Signs are greater than 6 and subtracted if the Signs are less than 6 . There is another method of computing Sheeghra Karna, the geocentric distance of the planet. . Sheeghra Karna can be computed by the following formula
c^2 = a^2 +b ^2 + 2 a b Cos A and the Sheegra Phalam can be obtained by
sin x = a Sin A /c for Jupiter, Mars and Saturn & sin x = b Sin A /c for Mercury and Venus
True Longitude of the Planet = Heliocentric Longitude of the Planet - or + Sheegra Phalam.
If the Mandaphalam is m and p is Parinathi Phalam and s is Sheegra Phalam, then Truelong = Meanlong + or - m + or - p + or - s
For Mercury and Venus, the computation is slightly different. The Sheeghra Phalam thus obtained is subtracted from the Sun's longitude if the Signs are more than 6 and added if the Signs are less than 6.
This method of Longitudes Corrected Thrice is highlighted in Puliyoor's Ganitha Nirnaya and Bhaskara's Ganitha Adhyaya. Achyuta Pisharody's Sphuta Nirnaya also deals with the calculations in Indian Astronomy. Other reference books are Maha Bhaskareeya, Aryabhateeya and Brahma Sphuta Siddhanta.
In Mathematics there are many methods and the Western Method is to find the True Anomaly of the Planet and to it add the Argument of Perihelion ( Long = v + w ). The Eccentric Anomaly of the Planet ( an auxiliary angle used in Kepler's equations ) is computed from the Mean Anomaly and the True Anomaly is computed from it . The Argument of Perihelion is added to it to get the true longitude. v is the Angle between the Planet and Perihelion and w is the angle between the Node and Perihelion. The perturbations of the Moon, Jupiter and Saturn are included in these computations. Some large perturbations of the Moon, viz the Evection, the Annual Equation, the Variation and the Parallactic Equation, with the equations of the Center, are all included. While the Western Method is to give 12 corrections to the Moon's longitude, the Vedic method is to subject the Mean longitude of the Moon to 16 trignometric corrections. ( 14 reductions plus Manda Kriya & Parinathi Kriya ). Then find out the Cartesian coordinates, x,y and z and then convert it to Spherical Coordinates, r, Theta and Phi. This Western method is not at all similar to the Indian one.
In essence, the Vedic Mathematical Method is to subject the Mean Longitude of the Planet to three major trignometric reductions. Also the other planets. Our friend Paul Schylter has done a great work in computing the Planetary Positions as per the Western System. Our congratulations to him. Here we give the Vedic Method as expounded by Aryabhata, Bhaskara, Brahmagupta, Madhava, Jyesthtadeva, Parameswara and countless other Vedic astronomers in the 18 Siddhantas ( treatises on Astronomy), written 5000 years ago !
|
 By
By