Indian Spherical Trignometry 

 

                                                                   

                                                                                                             

Jya ( Sine ), Kotijya ( Cosine ) and Utkram Jya ( Versine ) are the three trignometric functions introduced by the Indian astronomers and mathematicians.

In order to compute the celestial longitudes of planets, these functions were used by the trinity of Indian Astronomy, Bhaskara, Brahnmagupta and Aryabhata.

Thrijya, the Radius or R

 

If Circumference = 2 Pi r 

360 = 2 Pi r

r = 360/2Pi in degrees

 r = 180/Pi

360*60 minutes  = 21600 minutes 

r = 21600 /2 Pi = 3438 minutes = 3438*60 =  206265 seconds 

( One degree is 60 minutes and one minute is 60 seconds and hence one degree is 3600 seconds.)

R in seconds will be ((360/2pi)* 3600 ) Vikalas or 206265 seconds. This figure 206265 is known as the Magic Figure of Astronomy.

Arybhata based his famous Sine tables on R = 3438 minutes and he gave the Jya ( modern Sine ) values of  Kakshyas  of 3 degrees and 45 minuts ( 30 degrees / 8 ) .

 

 

Bhujajya = R Sin
Kotijya = R Cos

The arc sine of the angle is Bhujachapa 
The arc cosine of the angle is Kotichapa
The arc tangent of the angle is Sparshachapa

By Jya, Bramhmagupta meant 5 degrees of a sign of 30 degrees. Hence a Zodiacal Sign consists of 6 Jyas ( 30 degrees ) . The Zodiac of 360 degrees was divided into 4 quarters of 90 degrees each. Three Jyas of 30 degrees each becomes a quadrant of the Zodiac and was called Thrijya. Thrijya is also the Radius, theVyasardha.

His magnum opus, the Brahmasphuta Siddhanta was translated by the Arabs as As Sind Hind. Jya became jiba and Kotijya became kojiba in Arabic. It was translated into Latin as sinus ( meaning ” bosom ” ). So Sinus and Co-sinus when translated into English became Sine and Cosine !

The Aryabhateeyam of Aryabhata was translated by the Arabs as Al Arjabhat.Trignometry is derived from the Sanskrit Thrikonamithi and Geometry from Jyamithi !

There are four major methods of calculation in Astronomy

They are

Longitudes calculated along the Zodiac or Ecliptic - The Ecliptic System
Longitudes calculated along the Celestial Equator - The Equatorial System
Longitudes calculated along the Celestial Horizon - The Horizontal System
Longitudes calculated along the Celestial Meridian - The Meridian System

Longitude measured along the Kranti Vritta, the Ecliptic or Bha Chakra , the Zodiac is known as Kranti Vritteeya Sphuta, the true longitude of the planet.

Longitudes measured along the Vishuvat Vritta, the Celestial Equator is known asVishuvat Vritteeya Sphuta, Right Ascension.

Udaya Lagna, the Ascendent and Astha Lagna, the Descendent are measured along the Celestial Horizon,The Kshitija

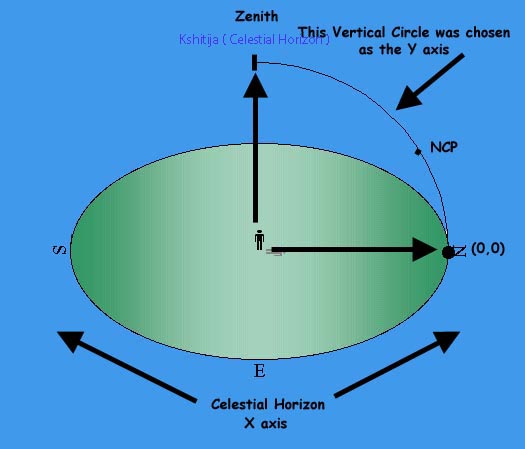
And the Madhya Lagna, the MC and the Patala Lagna, the IC are measured along the Celestial Meridian, the Nadi Vritta.

In order to compute the celestial longitudes of planets, first the Graha Madhyam, the mean longitude of the planet is computed.

We have to understand that the planets traverse in elliptical orbits. If their orbits are circular, then there is no need for jya samskaras ( trignometric corrections ).

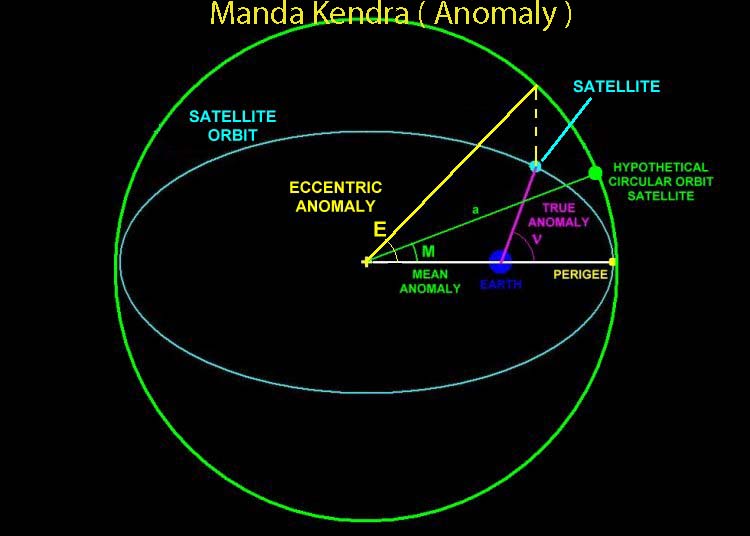
Once the mean longitudes of the planets are ascertained, then we first start with the First Jya Samskara, the first trignometric correction. Manda Jya means Sin M in Western Astronomy.

The Kepler Equation is M = E - e Sin E, where e is eccentricity and E is the Eccentric Anomaly, an auxilary angle in Kepler’s equations.

Like Kepler who brought in an auxiliary angle ( E, the Eccentric Anomaly ), Indian Astronomy uses Vikshepa Vritta, an auxiliary circle. The mean longitude of a planet reduced by Manda Kriya is the Vikshepa Vritteeya Sphuta, the once corrected longitude of the planet.

While Western astronomers compute the celestial longitudes using the formula Theta = v + w ( Celestial Longitude = True Anomaly + the Argument of Perihelion ), Indian astronomers use the Triune Trignometric Method. Longitudes are corrected thrice using Manda Kriya, Parinathi Kriya and Sheegra Kriya.

The perturbations of planets

All planets have perturbations. Moon has 300 perturbations, of which 14 are major. Hence for 14 perturbations, 14 jya samskaras have to be done ( Chatur Dasa Jya Samskara). The largest of them is the Evection. There are others like the Variation, the Annual Equation and the Parallactic Equation. When 14 trignometric corrections are done, we get the Reduced Longitude of the Moon, the Samskritha Chandra Madhyamam.

Jupiter has five major perturbations ( guror pancha kendrani bhavanthi ) and Saturn has six. So five jya samskaras and six jya samskaras have to be done for Jupiter and Saturn, before commencing the Triune Trignometric Method.